第128回コラム「家の鍵問題」
2021年3月22日
小山 裕司 教授
家の鍵を忘れ、家から締め出された経験はあるだろうか。私は何度もある。管理会社を呼び出したり、外泊したりと後始末が面倒で、さらに何より自ら反省し、気が滅いる。いい加減に懲りてスペアの鍵をカバンに常備したりし、最近は頻度が減ったものの、しかし悲しいことに数年に1度は起こる。最近、修了生のFB上の記事を参考にスマートロックを付けてみた。最近のものは、マンションのオートロックすら突破でき、またNFCタグを貼れば スマートフォンの操作すら不要で、まさに文明の利器だと感じている。しかし、生命線がスマートフォンに変わっただけだし、また無線LANが落ちても終わりである。震災で電気が止まり、電子マネー類が壊滅し、現金に戻った話を聞く。スマートロックは素晴らしいのだが、最悪の事態を想定すると混迷が深まってしまう。ハイテクからローテクに戻るが、3-4桁の数字回す錠付きの箱を設置し、鍵を収納するのはどうかと思ったりもする。マンションの下見での鍵の受け渡しに使ったりする奴である。
◎「総当り攻撃(Brute Force Attack)」
3桁鍵の数字並びは1,000通りあるので、丁寧に我慢強く総当り攻撃をされると、1処理1秒換算で最長1,000秒(16分40秒)で解除されてしまう。自転車の窃盗が多い訳だ。銀行、クレジットカード等のPIN(N: Personal Identification Number、暗証番号)は私が生まれた頃から伝統的に4桁である[1]。4桁の数字並びは10,000通りあるので、最長10,000秒(2時間46分40秒)かかるので、若干強度があがるように感じるが、物理的に数字を回すかわりにデジタル技術で総当り攻撃されると100秒かからず解除されてしまう(1処理0.01秒換算)。これは弱い。銀行等では、誕生日等の容易に推定できる4桁PINは避けるように再三指導される。自らの誕生日は当然であるが、日付にすることで4桁の数字並びは366通りに減ってしまう。月日を逆にするパターン込みでも588通りであり、3桁鍵の強度を下回る。これは弱すぎる。
4桁PINの推定は[1]で論じられている。この論文では、2009年にあるサイトから漏洩したアカウントのうち、約1800千の4桁PINを調べている。最頻度のPINは「1234」の3.7%、反対に「8439」は0.0006%であった。図1は4桁PINの前と後の2桁をXY座標に表示したものである。
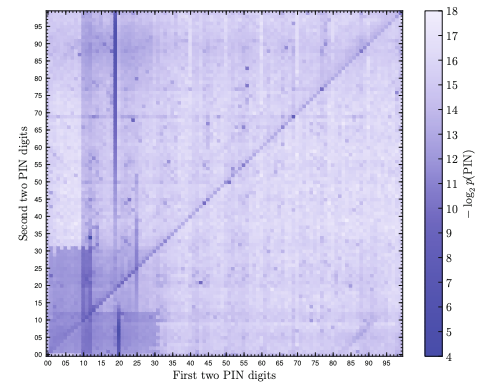
図1: RockYouから流出した4桁PINの分布図
出現頻度が高い4桁は濃く示され、
- 0101から1231までのMMDD書式、逆のDDMM書式での日付の範囲にあたる左下が濃い。したがって、31日及び2月の月末は薄い。
- 左下から右上への0000、0101、…、9898、9999等のABAB書式が目に付き、7777、8888等のAAAA書式も特に濃い。
- 左の縦線は1930から2010までの生まれた年である。
- 最頻度の1234のほか、2345、3456、4567、5678、2468、4321が濃い。
は容易に推定できる。さらにTwitter上では中央付近の5150はVan Halenのアルバムに起因する等の興味深い推測が行われた[2]。興味があれば自分が使っている4桁PINの濃さを確認してみるのもいいだろう。
◎「アーキテクチャによる統制」
PINの強度をあげるにはどうすればいいだろうか。次の仕組みがアーキテクチャによる統制として一般的である。
- 4桁PIN等、現在では弱すぎる認証では、総当たり攻撃に対して間違いの回数の上限を設定している。iOSで画面ロックの解除等のパスコードは6回間違うと1分待たされ、次は5分、15分、60分と待たされ、10回間違うとiTunes接続を指示され、最悪すべてデータが削除されてしまうらしい(試す元気は今日は無い)。この間違い回数の上限の設定にはすこし短所があって、第三者の操作であってもPINを何回か間違うとアカウントをロックできてしまう。実誰、私のあるアカウントが昨年誰かの操作によってロックされてしまった(悪意の有無はわかりませんが、面倒だから悪戯は止めてください)。
- iOSでは暗証番号の既定の桁数を4桁から6桁に変更した(6桁の数字並びは1,000,000通り)。最近は、暗証コードは数字大文字小文字8文字以上等の文字列という制約が課されることが多い(約2×10**14通り)。許されるのであれば、さらに記憶できるのであれば、長い暗証コードは正義である。数字だけの15桁は数字大文字小文字8文字より強い。
アーキテクチャの決定ではどちらを選択するのが正しいだろうか。またこのほかの仕組みとしては何が現実的だろうか。我々がアーキテクチャを決定する際には強度と使い勝手のバランスと、実装上の制約を考慮する必要がある。
◎「逆総当り攻撃(Reverse Brute Force Attack)」
金融機関の情報システム構築では、FISC(The Center for Financial Industry Information Systems)が定めた基準で、PINの間違いの回数の制限が定められ、不正攻撃にはアカウントのロックで防御する。しかし、昨年の夏頃、PINは「1234」等の決め打ちで逆にアカウントのほうを総当たりで連続して試す逆総当り攻撃が行われた可能性が指摘された。この攻撃では各アカウントに対する攻撃は数回だけだから上限の設定で防御することは難しい。高頻度PINはある程度わかっているので、これが成功する可能性は比較的高い。しかし、最近のアカウント管理では、AI等での振る舞いを監視していると聞く。
◎「離散数学の基礎」
当記事で何度か登場した「何通りあるかの計数(カウント)」は、離散数学の基礎であり、情報科学の典型例であるロック解除問題(Code Crack Problem)、旅商人問題(TSP: Traveling Salesman Problem)、nクイーン問題(n Queens Problem)等で必要とされ、また最近流行りのAI領域でも重要である。計数の基礎は、和・積の法則、置換、順列等として、中等教育の数学の範囲であるが、高等学校の数学の指導要領の変遷をざっと確認してみると、平成10-11年改定と昭和52-53年改定では、計数に関する内容が必修から外れていた。年齢でいうと、30歳前後(昭和62/4-平成8/3生まれ)と50歳前後(昭和41/4-昭和53/3生まれ、私のことか)の世代が相当する。また、必修であっても中等教育の数学等忘れてしまっている恐れもある。再度、高等学校の数学を振り返ってみるのもいいだろう。第1学期の「情報アーキテクチャ特論1」では、離散数学の基礎を振り返る内容を扱っているので、よろしければ是非。
[1] Joseph Bonneau, et al., A Birthday Present Every Eleven Wallets? The Security of Customer-Chosen Banking (2012). https://link.springer.com/chapter/10.1007/978-3-642-32946-3_3
